Modern encryption methods #
Symmetric encryption #
AES: Advanced Encryption Standard #
- Block Cipher with a block size of 128 bits
- There are three variants of key lengths, which differ only in the number of rounds
- 128 bit: 10 rounds
- 192 bit: 12 rounds
- 256 bit: 14 rounds
Intel CPUs support the Advanced Encryption Standard New Instructions(AES-NI) instruction set, which makes the algorithm faster by up to 13.5 times.
AES GCM enables plaintext encryption and guarantees the integrity of the generated ciphertext through a cryptographic checksum. AES GCM has a high data throughput because the encryption also includes the signature. On the one hand, all counter blocks can be precomputed once the IV and plaintext length are known. On the other hand, authentication of ciphertext blocks and encryption of other plaintext blocks can run in parallel.
The CTR Counter Mode is a mode in which block ciphers such as AES can be operated to produce a stream cipher. For encryption, an initialization vector is encrypted with the key to produce an intermediate key. This is then combined with the plaintext using an XOR operation. This produces the ciphertext.
Camellia #
Camellia uses the same parameters as AES: a block size of 128 bits and key lengths of 128, 192, or 256 bits. Camellia was developed in Japan and can be compared to AES. However, the hardware is more optimized for AES.
Asymmetric encryption #
RSA #
Rivest Shamir Adleman (RSA)](https://de.wikipedia.org/wiki/RSA-Kryptosystem) is an asymmetric cryptographic method that can be used for both encryption and digital signing.
RSA signature keys typically have a very small public exponent with only two bits set to 1. In contrast, the modulus and private exponent is very large, with about half of the bits set to 1. As a result, verification of the signature is much faster than generation.
Procedure #
- Choose two prime numbers and form the product: \(n = p * q\)
- \(φ(n) = (p-1) * (q-1)\)
- Choose arbitrary number a, where a must be divisor-unrelated to φ(n). That is, the \(ggt(φ(n), a) = 1\) . Prime numbers are best suited for a. A is the private key.
- Compute multiplicative inverse b: \(a * b = 1 \text{ mod(φ(n))}\) . This can be computed using the extended Euclidean algorithm. 1st modulus: n (public) 2. public key: b 3. private key: a
Then it can be used as follows:
\[value-encrypted = (value-unencrypted)^b * \text{ mod(n)}\] \[value-unencrypted = (value-encrypted)^a * \text{ mod(n)}\]
DH: Diffie-Hellman #
The DH key exchange is an asymmetric method used to generate a symmetric key. The idea behind this method is that the two partners generate the secret key together (Shared Master Secret) without having to transmit it entirely. In contrast to RSA, nothing can be signed with this method.
- One way function: \(f(x) = g^x \text{ mod(p)}\)
- The numbers g and p are public and can be transmitted unprotected
- Alice and Bob agree on the numbers g and p
- Alice chooses a random number a and sends Bob the computed value large A. \(A = g^a \text{ mod(p)}\)
- Bob chooses a random number b and sends Alice the calculated value large B. \(B = g^b \text{ mod(p)}\)
- Both can now compute the secret symmetric key K: \(K = A^b \text{ mod(p)}\) and \(K = B^a \text{ mod(p)}\)
Elliptic Curves #
- The key strength is always half of the specified key length. (e.g. ECDH256 is 128 bit strong).
- ECDSA is much faster than RSA
- With D-Wave 1000 Qbits are possible, but Shor’s Quantum Algorithm is not fulfilled, because not correct quantum states are used.
ECDH #
The cryptographic strength of the ECDH algorithm is based on the fact that it takes a lot of effort to find out the number of additions of a curve point P with itself modulo a prime number p (i.e., the n in \(n * P \text{ mod(p)} = (P1+P2+...+Pn) \text{ mod(p)}\) ). Basically, ECDH thus builds on the same or a very similar problem as DH and RSA. However, ECDH is resistant to some attacks that make the factorization of RSA/DH easier. As a result, much shorter keys are possible.
To disguise that photons have been stolen, an attacker could deliberately insert decoy states. As a countermeasure, the sender inserts random decoy states and tells the receiver which were the decoy states. The decoy states are sent out at a lower line level. If the attacker is on the line, a different statistical distribution (of data and decoy pulses) results, which in turn can be detected.
Quantum cryptography #
Ekert E91 protocol #
In the Ekerte E91 protocol, a laser generates an entangled pair of photons from time to time. When you measure the state of one, you know the state of the other. Both end stations must measure with the same filter set (vertical, horizontal). If several photons do not arrive (individual ones can be swallowed by the optical fiber), the receiver can assume that the line is being tapped.
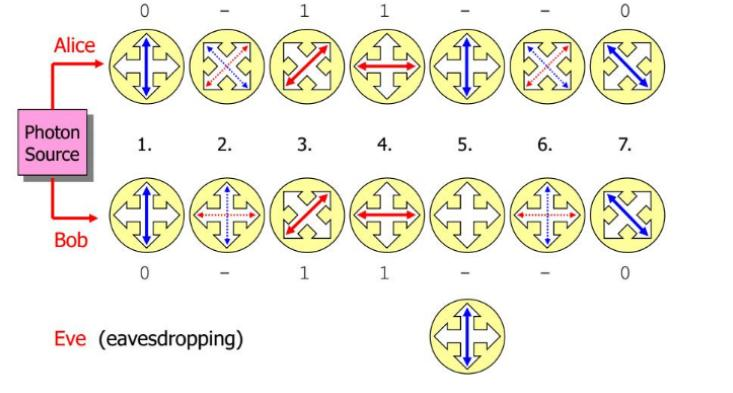
BB84 protocol #
With the BB84, no entangled photon pairs are needed. Here, only a single photon is sent, which can assume 4 states. Equally, likely is 45 degree polarization ( \(0^{\circ} \) , \(45^{\circ}\) , \(90^{\circ}\) and \(135^{\circ}\) ). Distances of 50-150km can be covered using this method.
The polarization of each photon received is measured by Bob using a random filter set (rectilinear or diagonal). After the measurements Bob announces over an unsecure channel, which channel which filter set he used to determine the polarization of each photon. Alice then announces for each transmitted photon whether it was rectilinear or diagonal polarized and whether it was a Decoy pulse or a normal pulse.
The larger the transmission distance, the more the bit slots without information increase. With a 1550nm wide fiber one has attenuation of 0.2dB/km. This results in the following losses:
- 50km: 10dB \(\rightarrow\) 1 of 10 photons survives
- 100km: 20dB \(\rightarrow\) 1 of 100 photons survives
- 150km: 30dB \(\rightarrow\) 1 of 1000 photons survived
Shor’s Quantum Algorithm #
For a number \(n\) , one needs a quantum computer with \(\log(n)\) qubits.
Grover’s Quantum Algorithm #
Grover’s algorithm proves that quantum computers are faster than classical computers in principle.
Quantum Resistant Algorithms #
For AES, it has been proven that the use of quantum computing cuts the key length in half. Therefore, a simple solution to the problem is to use key lengths that are twice as large.