Cryptoanalysis #

Originally, cryptanalysis was the study of methods and techniques, to extract information from encrypted texts. Today one speaks analysis to break encryption or to prove or quantify its security.

Frequency analysis #

Can be used for the simple substitution methods. Thereby from an auxiliary text the letter frequency is determined. This can be for example a German fairy tale or something similar. In the German language the letter e is the most frequent character. The analysis takes advantage of the fact that a plaintext letter is always converted to the same ciphertext letter. The frequency of the ciphertext letters is determined and applied to the letter frequency of the help text.

Buchstabenhäufigkeit deutschsprachiger Texte von Loki_66 - Eigenes Werk, Tabelle CC BY-SA 3.0, Link

Autocorrelation #

Autocorrelation can be better explained by examples. It can be calculated manually, of course.

First, the string to be examined is written down in a line. Then below it the shifted string is written. Now the matches are counted. For each shift this would have to be done, so that a diagram like the one below can be created.

Shift with only one character #

Example with the string “aaaaaaaa” (10 times the letter a).

Shift 0:

aaaaaaaaaa
aaaaaaaaaa

The match is 10 (or 100%)

Shift 1:

aaaaaaaaaa
 aaaaaaaaaa

The match is 9 (or 90%).

Graphically, this would look like this with many shifts:

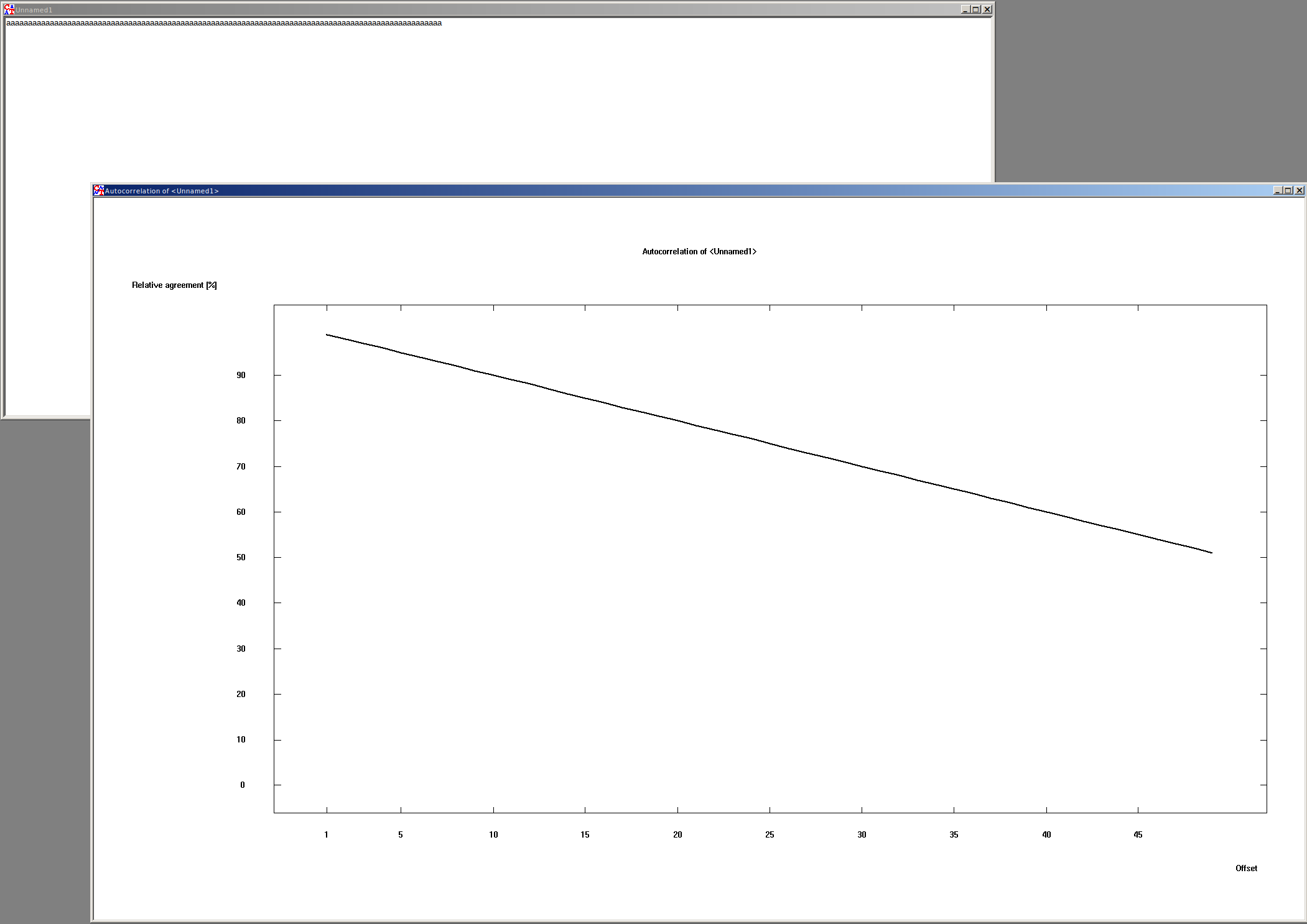
Autokorrelation with one letter. Eine decreasing line

Shift of repeating characters #

With repeating strings it looks like:

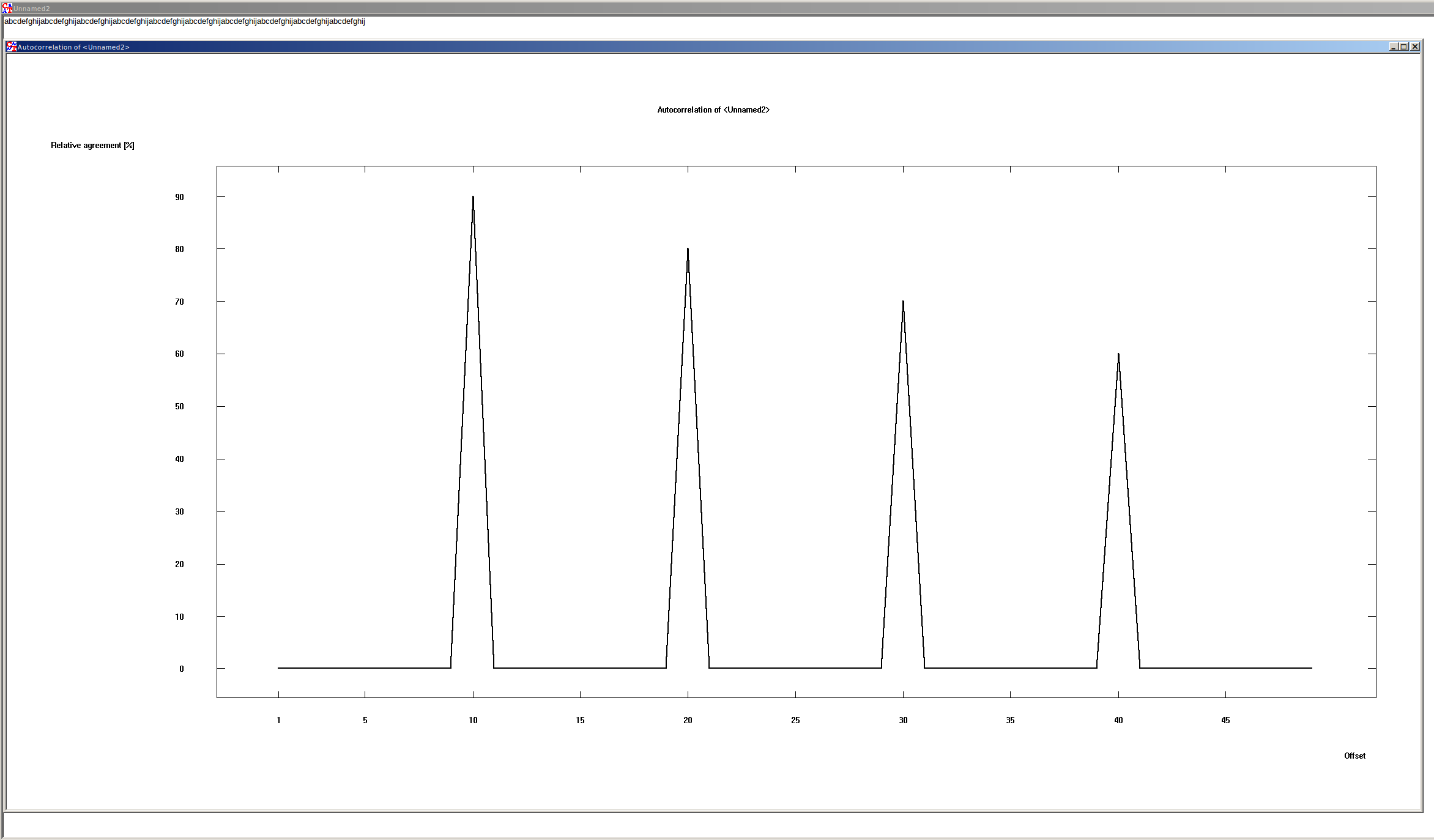
Autocorrelation with repeating characters. Leads to peaks that become smaller

There are a couple of interesting things in the graph.

The peaks show the highest match in each case, first at 10. This is because the string is 10 characters long and then repeats itself.

The peaks get smaller and smaller each time. This is because the text is shifted by itself. So with each shift characters are pushed out and there must then be fewer and fewer matches.

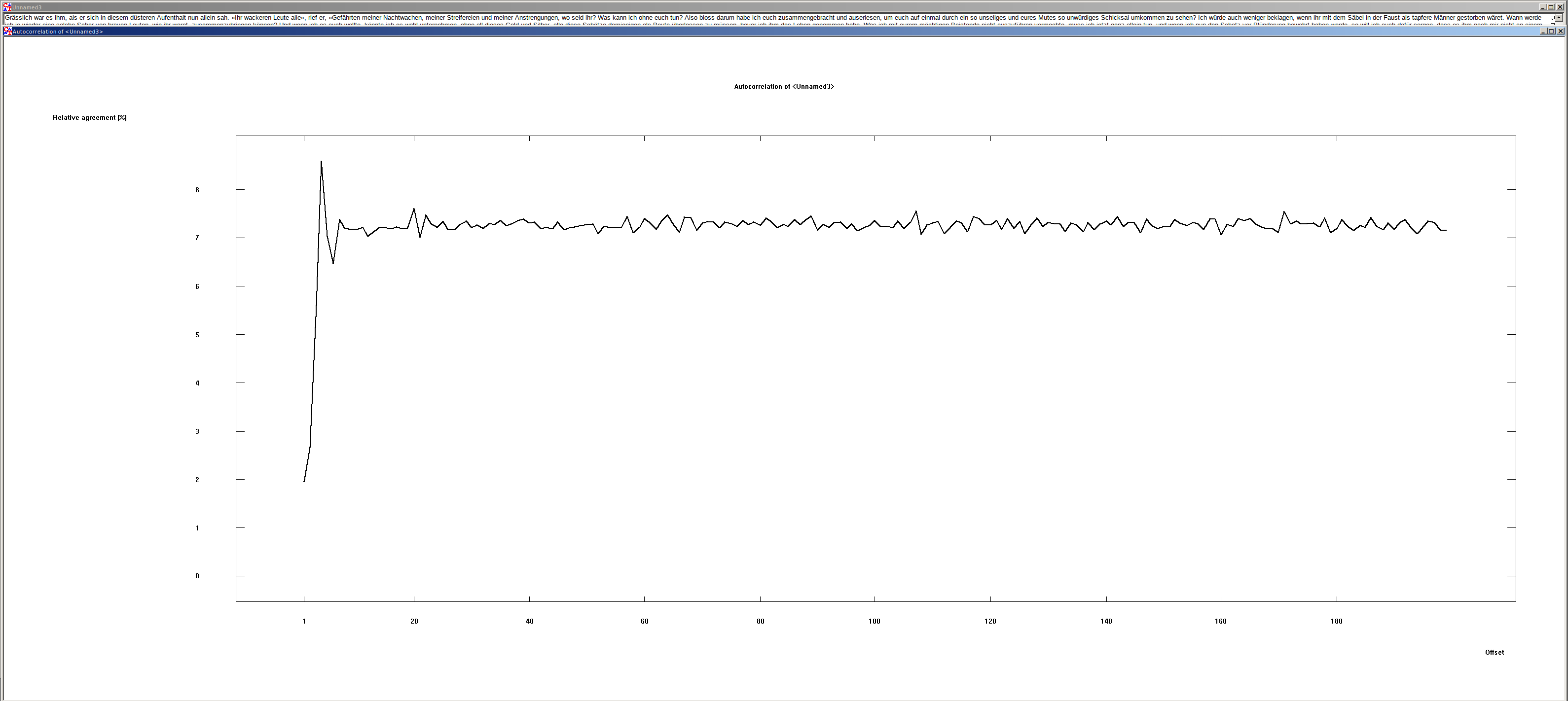
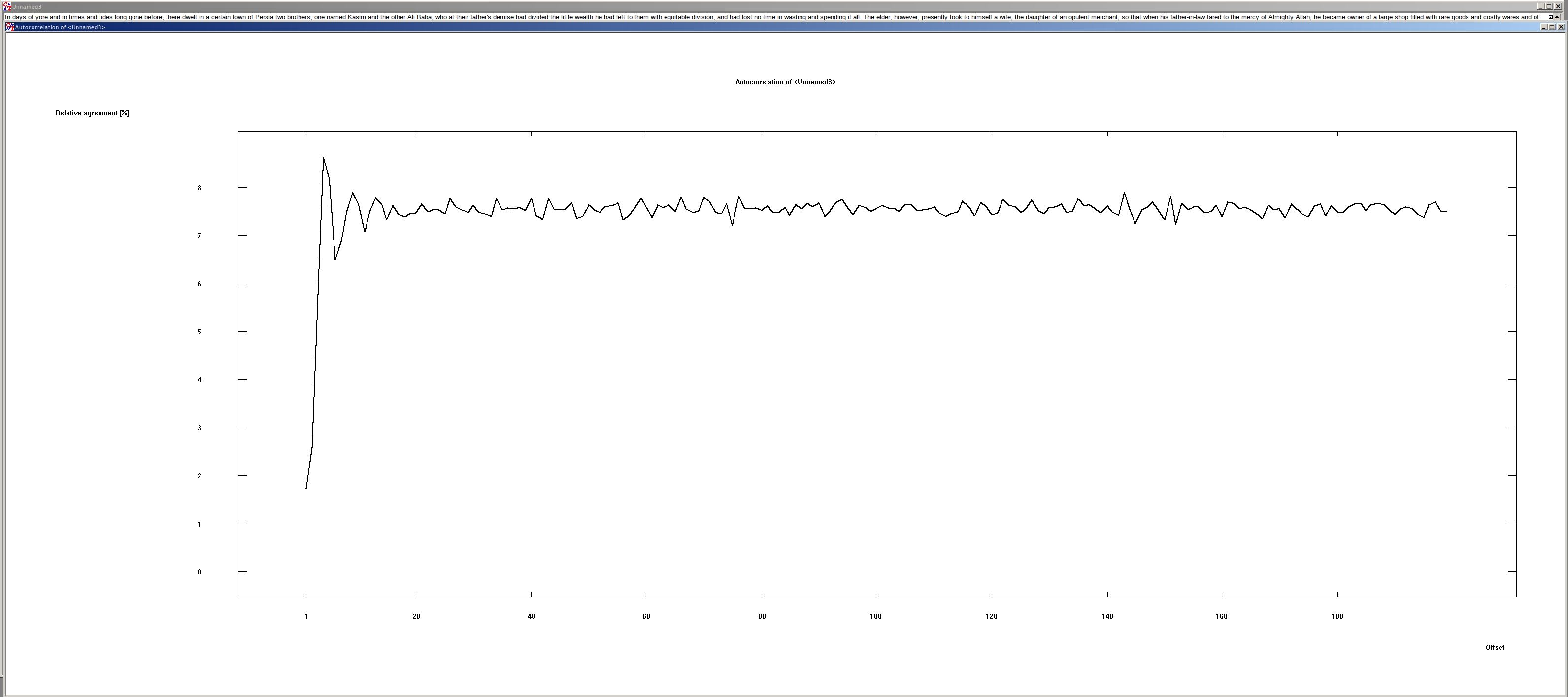
Shifting of German and English texts #

The shift by one character is interesting. Here you can see that the match is very small. The reason lies in the character distribution of the written languages. In the German and English language character doubles are rather rare. But exactly these are needed, so that it comes to a match.

Furthermore, it is to be seen that the agreement of the text with each shift > 1 is about 7.6 %. This value can be used to recognize plaintexts by machine.

Autocorrelation of a German text. Leads to noise at 7.6 percent Autocorrelation of an English text. Leads to noise at 7.6 percent

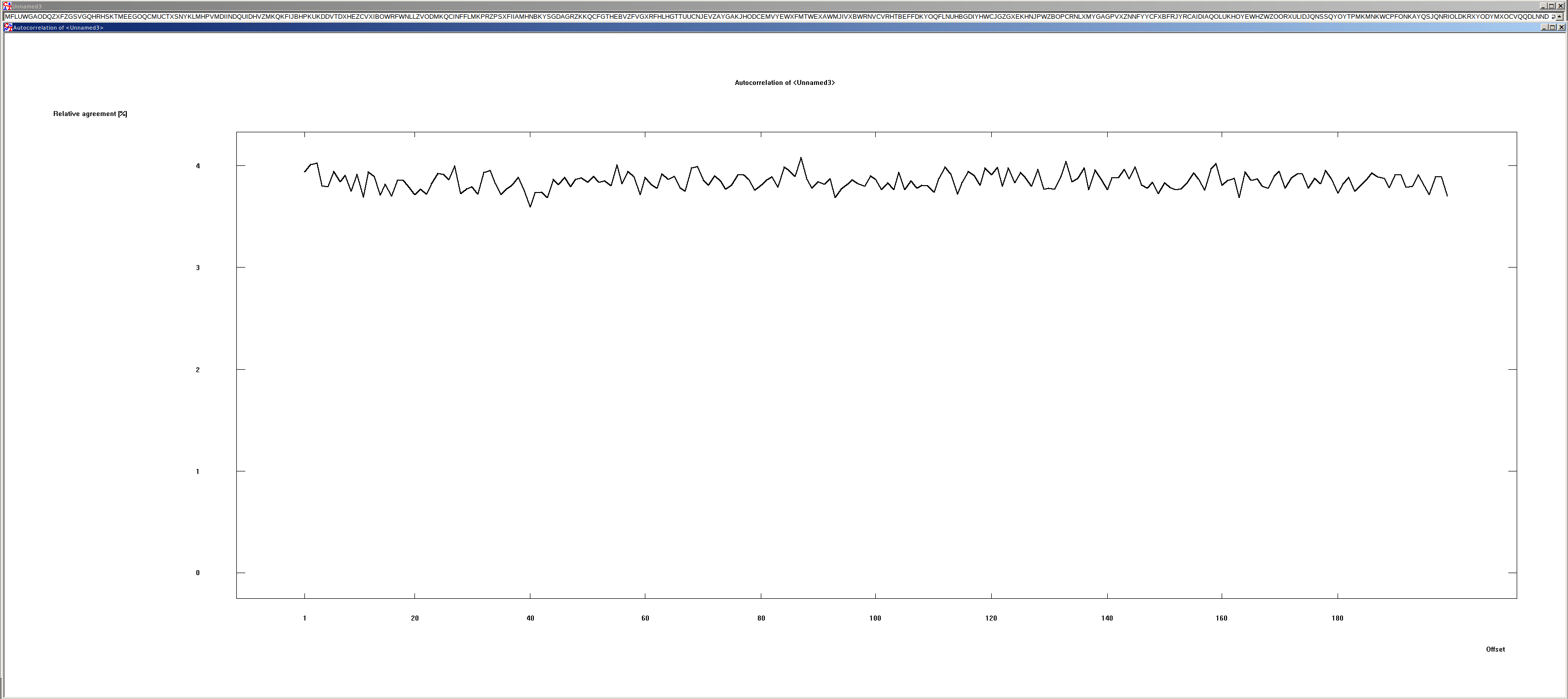
Shifting random strings #

There are 26 different characters in this text. The probability is 1/26, or 3.8 %. This can also be seen in the graphic:

autocorrelation of a random text leads to noise at about 3.8 percent
(1/26)