Moderne Verschlüsslungsverfahren #

Symmetrische Verschlüsselung #

AES: Advanced Encryption Standard #

• Block Cipher mit einer Blockgrösse von 128 Bit
• Es gibt drei Varianten von Schlüssellängen, welche sich nur in den Anzahl Runden unterscheiden
  1. 128 Bit: 10 Runden
  2. 192 Bit: 12 Runden
  3. 256 Bit: 14 Runden

Intel CPUs unterstützen das Advanced Encryption Standard New Instructions(AES-NI) Instruktionsset, das den Algorithmus um bis 13.5 Mal schneller macht.

AES GCM ermöglicht eine Verschlüsselung des Plaintextes und garantiert die Integrität des generierten Ciphertextes durch eine kryptographische Checksumme. AES GCM hat einen hohen Datendurchsatz, weil in der Verschlüsselung auch die Signatur beinhaltet ist. Einerseits können alle Counter-Blöcke vorberechnet werden, sobald der IV und die Plaintext-Länge bekannt sind. Andererseits kann die Authentisierung von Ciphertext-Blöcken und die Verschlüsselung von weiteren Plaintext-Blöcken parallel ablaufen.

Der CTR Counter Mode ist eine Betriebsart, in der Blockchiffren wie AES betrieben werden können, um daraus eine Stromchiffre zu erzeugen. Zur Verschlüsselung wird ein Initialisierungsvektor mit dem Schlüssel verschlüsselt und so ein Zwischenschlüssel produziert. Dieser wird im Anschluss mittels einer XOR-Operation mit dem Klartext kombiniert. Daraus entsteht der Geheimtext.

Camellia #

Camellia verwendet die gleichen Parameter wie AES: eine Blockgröße von 128 Bit und Schlüssellängen von 128, 192 oder 256 Bit. Camellia wurde in Japan entwickelt und kann mit AES verglichen werden. Die Hardware ist aber eher für AES optimiert.

Asymmetrische Verschlüsselung #

RSA #

Rivest Shamir Adleman (RSA) ist ein asymmetrisches kryptographisches Verfahren, das sowohl zum Verschlüsseln als auch zum digitalen Signieren verwendet werden kann.

RSA Signatur Schlüssel haben üblicherweise einen sehr kleinen öffentlichen Exponenten, bei dem nur zwei Bits auf 1 gesetzt sind. Im Gegensatz dazu ist das Modul und der private Exponent sehr gross, bei dem etwa die Hälfte der Bits auf 1 gesetzt sind. Daraus resultiert, dass die Verifikation der Signatur sehr viel schneller geht, wie die Generierung.

Vorgehen #

1. Zwei Primzahlen wählen und Produkt bilden: \(n = p * q\)
2. \(φ(n) = (p−1) * (q−1)\)
3. Beliebige Zahl a wählen, wobei a teilerfremd zu φ(n) sein muss. Das heisst, dass der \(ggt(φ(n), a) = 1\) . Am besten eignen sich Primzahlen für a. A ist der private Schlüssel.
4. Multiplikative Inverse b berechnen: \(a * b = 1 \text{ mod(φ(n))}\) . Das kann mit dem erweiterter Euklidischer Algorithmus berechnet werden.
   1. Modul: n (öffentlich)
   2. Öffentlicher Schlüssel: b
   3. Privater Schlüssel: a

Anschliessend kann es wie folgt verwendet werden:

\(Wertverschlüsselt = (Wertunverschlüsselt)^b * \text{ mod(n)}\) \(Wertunverschlüsselt = (Wertverschlüsselt)^a * \text{ mod(n)}\)

DH: Diffie-Hellman #

Der DH Schüsselaustausch ist ein asymmetrisches Verfahren, das dazu verwendet wird, einen symmetrischen Key zu generieren. Die Idee hinter diesem Verfahren ist, dass die beide Partner gemeinsam den geheimen Schlüssel generieren (Shared Master Secret) ohne ihn ganz übermitteln zu müssen. Im Gegensatz zu RSA kann mit diesem Verfahren nichts signiert werden.

1. One Way Function: \(f(x) = g^x \text{ mod(p)}\)
2. Die Zahlen g und p sind öffentlich und können ungeschützt übertragen werden
3. Alice und Bob einigen sich auf die Zahlen g und p
4. Alice wählt eine zufällige Zahl a und sendet Bob den berechneten Wert gross A. \(A = g^a \text{ mod(p)}\)
5. Bob wählt eine zufällige Zahl b und sendet Alice den berechneten Wert gross B. \(B = g^b \text{ mod(p)}\)
6. Beide können nun den geheimen symmetrischen Schlüssel K berechnen: \(K = A^b \text{ mod(p)}\) und \(K = B^a \text{ mod(p)}\)

Elliptic Curves #

• Die Schlüsselstärke ist immer die Hälfte der angegeben Schlüssellänge. (z.B ECDH256 ist 128 bit stark)
• ECDSA ist wesentlich schneller wie RSA
• Mit dem D-Wave sind 1000 Qbits möglich, jedoch wird der Shor’s Quantum Algorithm nicht erfüllt, da nicht richtige Quantenzustände verwendet werden.

ECDH #

Die kryptografische Stärke des ECDH Algorithmus beruht darauf, dass es sehr aufwändig ist, die Anzahl Additionen eines Kurvenpunktes P mit sich selber Modulo einer Primzahl p (d.h., das n in \(n * P \text{ mod(p)} = (P1+P2+...+Pn) \text{ mod(p)})\) herauszufinden. Grundsätzlich baut ECDH damit auf das gleiche bzw. ein sehr ähnliches Problem wie DH und RSA auf. Allerdings ist ECDH gegen einige Angriffe resistent, die die Faktorisierung von RSA/DH einfacher machen. Dadurch sind deutlich kürzere Schlüssel möglich.

Um zu verschleiern, dass Photonen gestohlen wurden, könnte ein Angreifer bewusst Decoy States einfügen. Als Gegenmassnahme fügt der Sender zufällige Decoy States ein und sagt dem Empfänger, welches die Decoy States waren. Die Decoy States werden auf einem niedrigeren Leitungspegel ausgesendet. Wenn der Angreifer auf der Leitung sitzt, resultiert eine andere statistische Verteilung (von Daten und Decoy Pulsen), was wiederum erkannt werden kann.

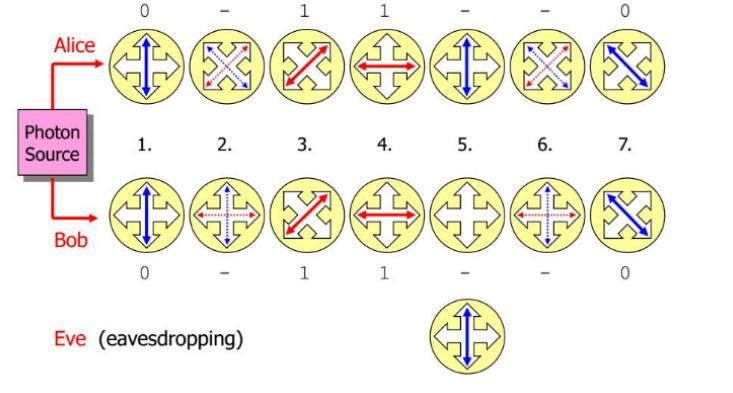
Quanten Kryptographie #

Ekert E91 Protokoll #

Beim Ekerte E91 Protokoll erzeugt ein Laser von Zeit zu Zeit ein verschränktes (entangled) Photonenpaar. Wenn man den Zustand des einen misst, kennt man den Zustand des anderen. Beide Endstationen müssen mit dem gleichen Filterset messen (vertikal, horizontal). Wenn mehrere Photonen nicht ankommen (einzelne können von der Glasfaser geschluckt werden), kann der Empfänger davon ausgehen, dass die Leitung abgehört wird.

BB84 Protokoll #

Beim BB84 braucht man keine verschränkte Photonenpaare. Hier wird nur ein einzelnes Photon versendet, das 4 Zustände annehmen kann. Gleichwahrscheinlich ist 45 Grad Polarisationen ( \(0^{\circ}\) , \(45^{\circ}\) , \(90^{\circ}\) und \(135^{\circ}\) ). Mit diesem Verfahren können Distanzen von 50-150km überwunden werden.

Die Polarisation jedes empfangen Photons wird von Bob mit einem zufällig gewählten Filterset gemessen (Rectilinear oder Diagonal). Nach den erfolgten Messungen gibt Bob über einen unsicheren Kanal bekannt, welches Filterset er jeweils für die Polarisationsbestimmung jedes Photons verwendet hat. Alice gibt anschliessend für jedes gesendete Photon bekannt, ob es rectilinear oder diagonal polarisiert wurde und ob es sich um einen Decoy-Puls oder einen normalen Puls gehandelt hat.

Je grösser die Übertragungsdistanz ist, desto mehr nehmen die Bit Slots ohne Information zu. Bei einer 1550nm breiten Fiber hat man Dämpfung von 0.2dB/km. Daraus resultieren folgende Verluste:

• 50km: 10dB \(\rightarrow\) 1 von 10 Photonen überlebt
• 100km: 20dB \(\rightarrow\) 1 von 100 Photonen überlebt
• 150km: 30dB \(\rightarrow\) 1 von 1000 Photonen überlebt

Shor’s Quantum Algorithm #

Für eine Zahl \(n\) benötigt man einen Quantencomputer mit \(\log(n)\) Qubits.

Grovers’s Quantum Algorithm #

Der Grover-Algorithmus beweist, dass Quantencomputer prinzipiell schneller als klassische Computer sind.

Quantenresistente Algorithmen #

Für AES wurde nachgewiesen, dass der Einsatz von Quantencomputer die Schlüssellänge halbiert. Eine einfache Lösung für das Problem ist deshalb, dass man doppelt so grosse Schlüssellängen verwendet.