Kryptoanalyse #

Ursprünglich war die Kryptoanalyse das Studium von Methoden und Techniken, um Informationen aus verschlüsselten Texten zu gewinnen. Heute spricht man eher von der Analyse zum Brechen der Verschlüsselung oder um ihre Sicherheit nachzuweisen, beziehungsweise zu quantifizieren.

Häufigkeitsanalyse #

Kann für die einfachen Substitutionsverfahren verwendet werden. Dabei wird von einem Hilfstext die Buchstabenhäufigkeit bestimmt. Das kann zum Beispiel ein deutsches Märchen oder etwas Ähnliches sein. In der deutschen Sprache ist der Buchstabe e das häufigste Zeichen. Die Analyse nützt aus, dass ein Klartext-Buchstabe immer zum gleichen Chiffratbuchstaben umgewandelt wird. Es wird also die Häufigkeit der Chiffratbuchstaben bestimmt und auf die Buchstabenhäufigkeit des Hilfstextes übersetzt.

Autokorrelation #

Die Autokorrelation lässt sich besser anhand von Beispielen erklären. Sie lässt sich natürlich auch händisch berechnen.

Zuerst wird die untersuchende Zeichenkette in einer Linie aufgeschrieben. Darunter wird dann die verschobene Zeichenkette geschrieben. Nun werden die Übereinstimmungen gezählt. Für jede Verschiebung müsste das gemacht werden, damit ein Diagramm wie unten aufgeführt entstehen kann.

Verschiebung mit nur einem Zeichen #

Beispiel mit der Zeichenkette “aaaaaaaaaa” (10 Mal der Buchstabe a).

Verschiebung 0:

aaaaaaaaaa
aaaaaaaaaa

Die Übereinstimmung beträgt 10 (bzw. 100%)

Verschiebung 1:

aaaaaaaaaa
 aaaaaaaaaa

Die Übereinstimmung beträg 9 (bzw. 90%)

Grafisch würde dies bei vielen Verschiebungen so aussehen:

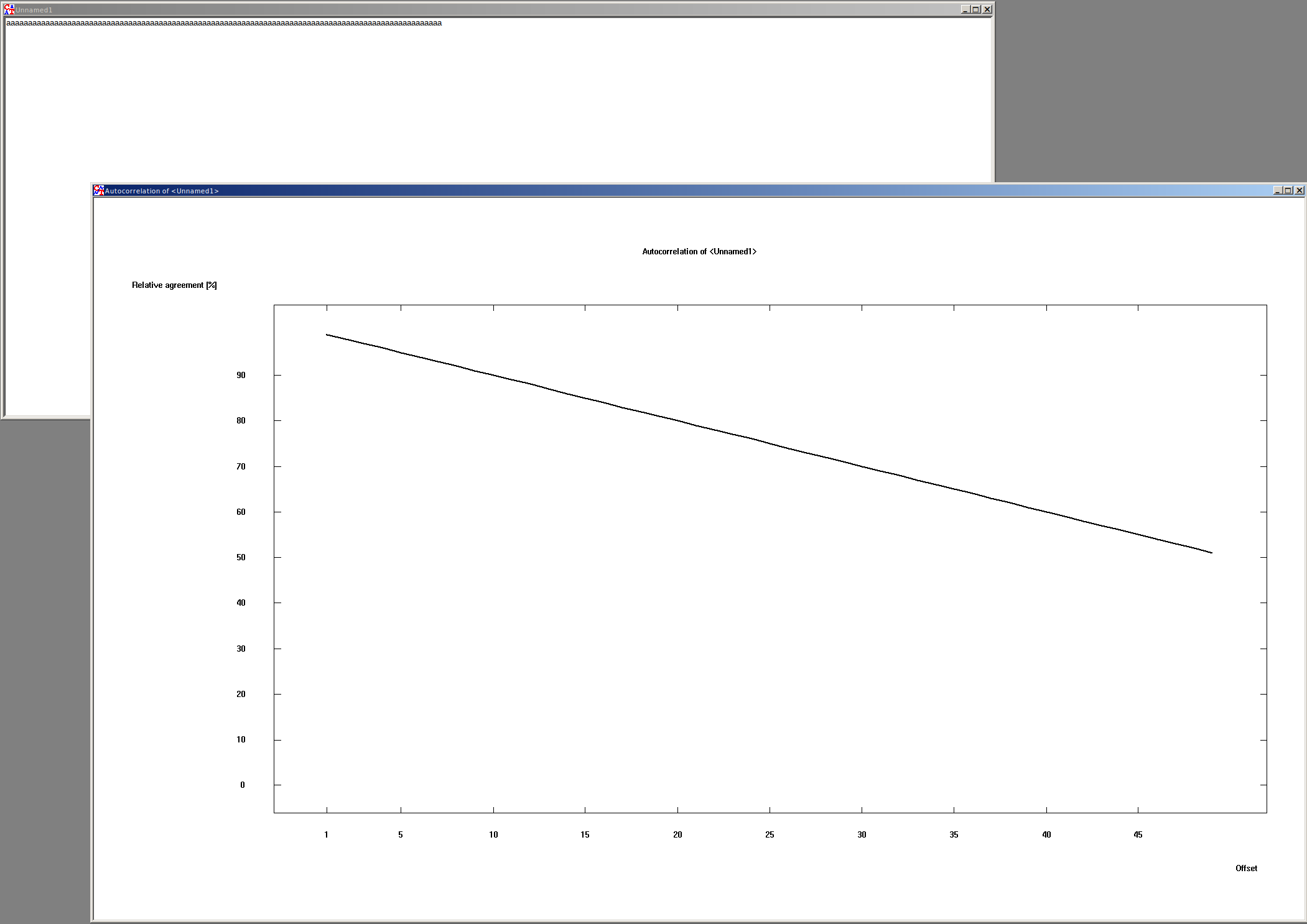
Verschiebung sich wiederholender Zeichen #

Bei sich wiederholenden Zeichenfolgen sieht es es aus:

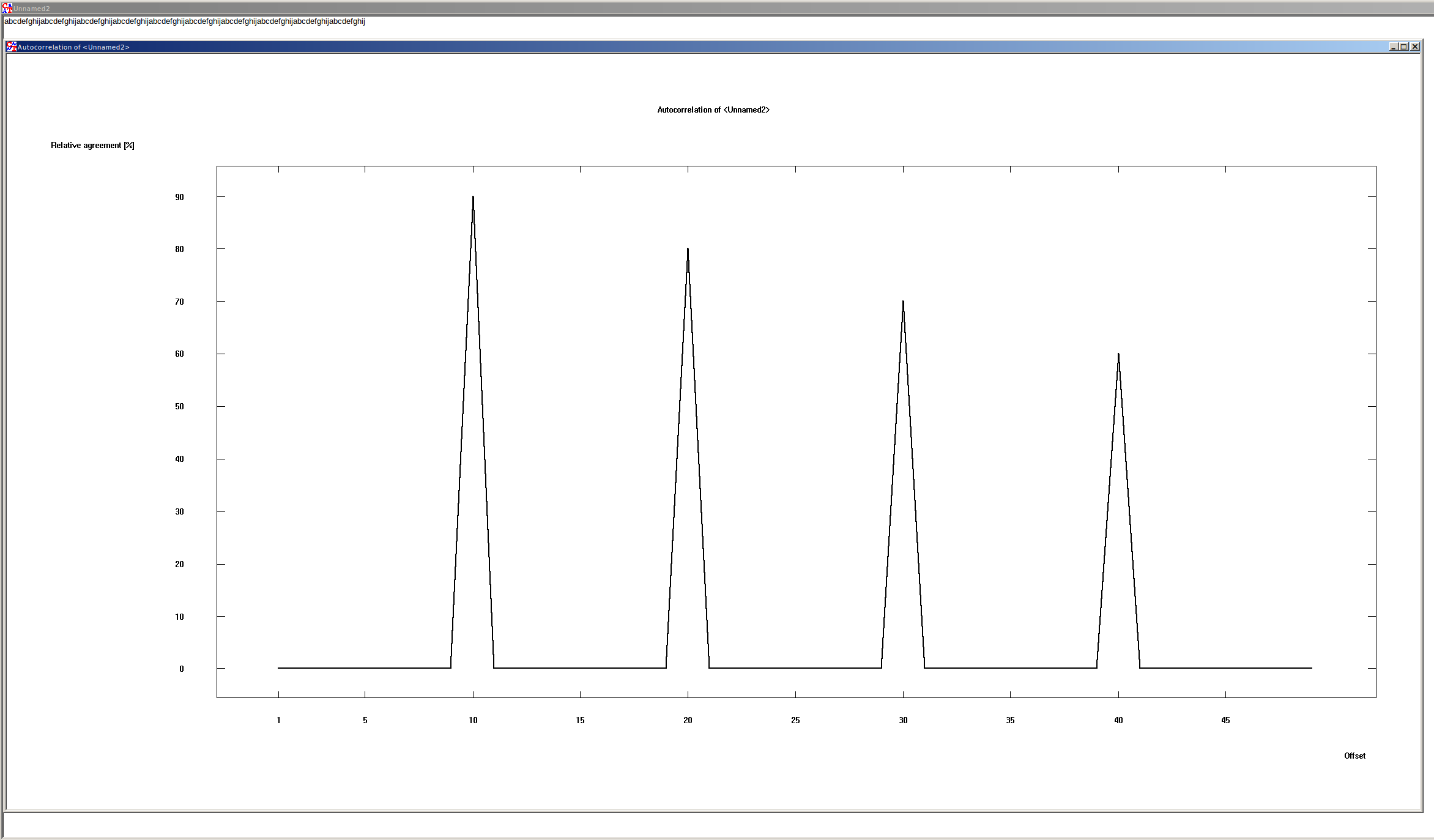
In der Grafik sind ein paar interessante Dinge zu erkennen.

Die Spitzen zeigen die jeweils höchste Übereinstimmung, erstmals bei 10. Dies liegt daran, dass die Zeichenfolge 10 Zeichen lang ist und sich dann wiederholt.

Die Spitzen werden jeweils immer kleiner. Das liegt daran, dass der Text mit sich selbst verschoben wird. Es werden also bei jeder Verschiebung Zeichen raus geschoben und es muss dann immer weniger Übereinstimmung geben.

Verschiebung von deutschen und englischen Texten #

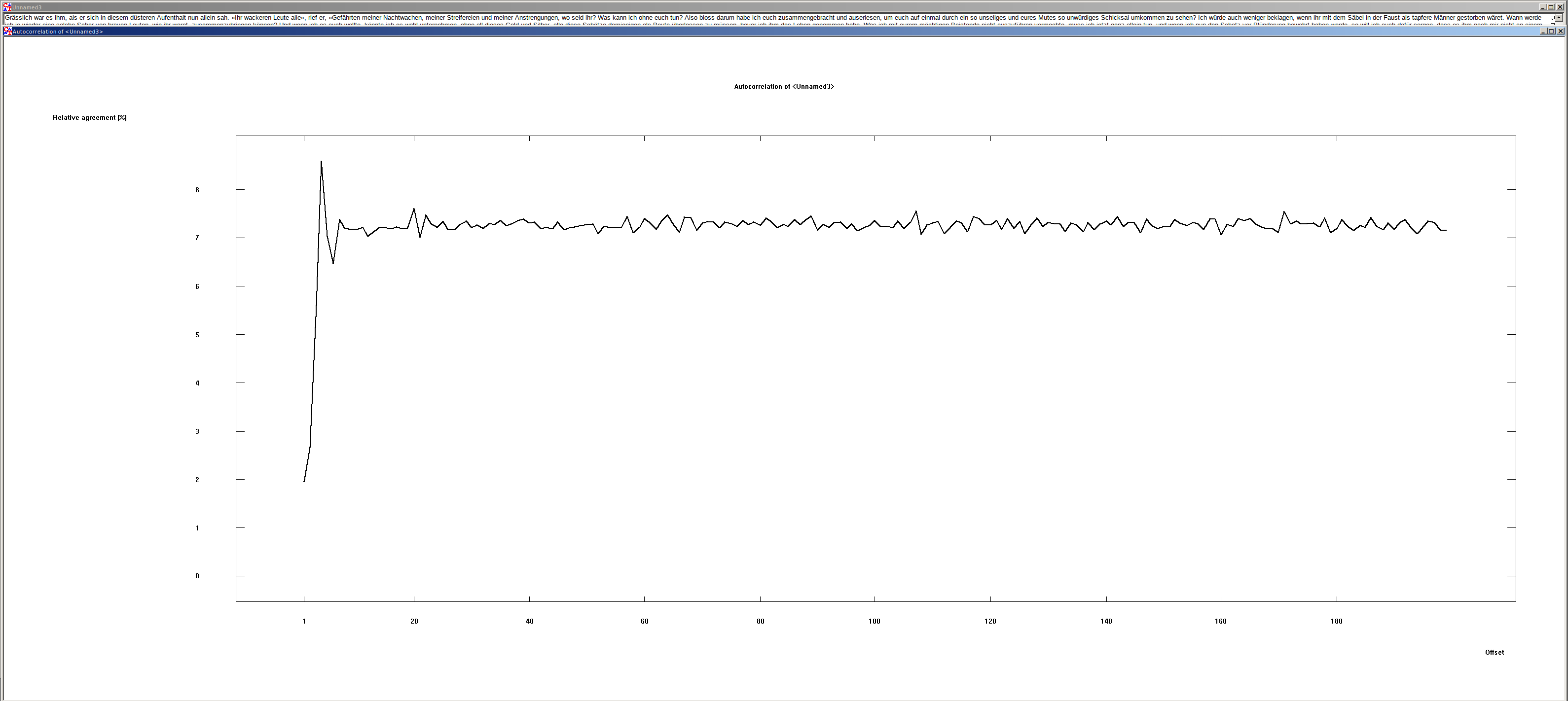
Interessant ist die Verschiebung um ein Zeichen. Hier ist zu sehen, dass die Übereinstimmung sehr klein ist. Der Grund liegt in der Zeichenverteilung der Schriftsprachen. In der deutschen und englischen Sprache sind Zeichendoppel eher selten. Doch genau diese werden benötigt, damit es zu einer Übereinstimmung kommt.

Des Weiteren ist zu sehen, dass die Übereinstimmung der Text bei jeder Verschiebung > 1 etwa 7.6 % ist. Dieser Wert kann verwendet werden, um Klartexte maschinell zu erkennen.

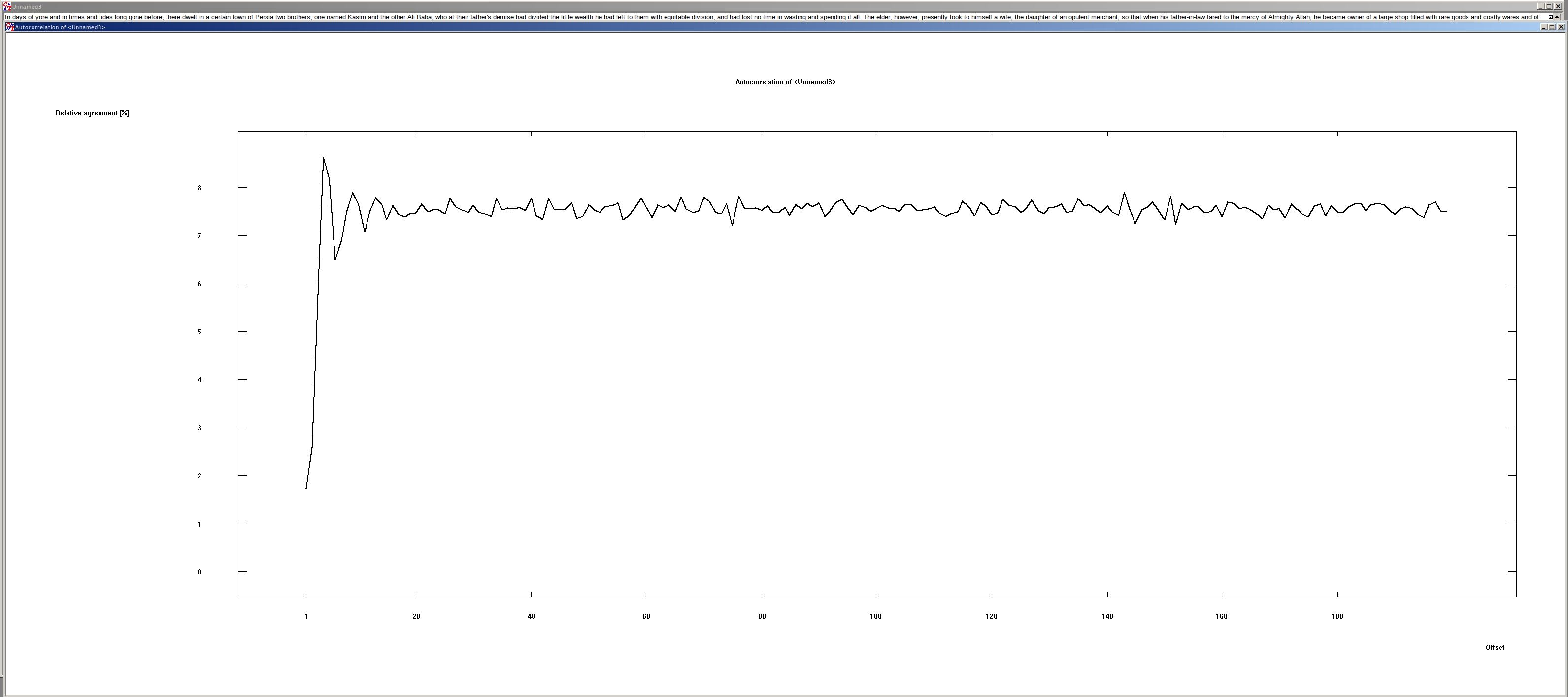
Verschiebung von Zufallszeichenfolgen #

In diesem Text kommen 26 verschiedene Zeichen vor. Die Wahrscheinlichkeit beträgt also 1/26, beziehungsweise 3.8 %. Dies ist auch in der Grafik zu erkennen: