Bloom-Filter#
Ein Bloom-Filter kann eingesetzt werden, wenn schnell überprüfbar sein muss, ob ein Wert nicht vorhanden ist. Man kann zum Beispiel verschiedene Wörter im Bloom-Filter speichern und schnell überprüfen, ob die Eingabe einem Wort im Filter entspricht. Der Vorteil vom Bloom-Filter ist der geringe Speicherplatz und die Geschwindigkeit. Ein Nachteil ist, dass mithilfe des Bloom-Filters nicht gesagt werden kann, ob der Wert vorhanden ist.
Hier mal ein kurzes Beispiel mit einzelnen Buchstaben:
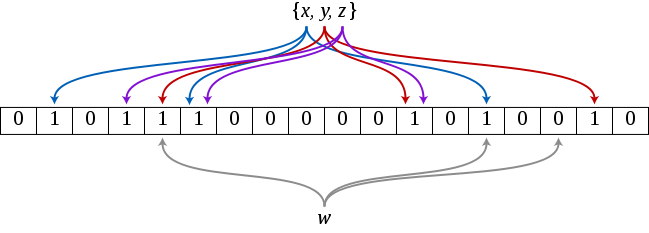
Bloomfilter von https://en.wikipedia.org/wiki/Bloom_filter#/media/File:Bloom_filter.svg lizenziert unter Public Domain
Im Filter befinden sich 3 Wörter (allg. n-Wörter) nämlich “x”, “y” und “z”. Der obige Filter besteht aus 18 Feldern (allg. m-Feldern) mit je einem Bit. Ausserdem werden 3 Hash-Funktionen verwendet (allg. k-Hash-Funktionen).
Wenn ein Wort im Bloom-Filter gespeichert werden soll, muss sich der Entwickler zuerst überlegen wie er das Wort in den Bereich [0; m) bringt. Das wird mit einer Hash-Funktion gemacht, die auch noch gleichverteilte Ergebnisse liefern muss. Das Ergebnis der Hash-Funktion zeigt also auf die Position im Array, die auf 1 gestellt werden muss.
Damit die Wahrscheinlichkeit von Kollisionen kleiner wird, werden mehrere Hash-Funktionen verwendet. Wenn beispielsweise die Hashfunktion f(x) = x % 5 lautet und die zwei Wörter 5 und 15 gehasht werden, dann führt das zu einer Kollision im Feld 0. Wenn aber zusätzlich noch eine zweite Hashfunktion g(x) = x % 6 hinzugefügt wird, ergibt das dann die Indices 5 und 3. Durch diese zweite Hash-Funktion wird also schon ein False-Positive verhindert.
Im obigen Beispiel sind die Hash-Werte des Wortes “w” {1, 5, 13}, für “y” dann {4, 11, 16} und für z dann {3, 5, 11}. Das Wort “w” befindet sich definitiv nicht im Bloom-Filter, da ein Hash-Wert auf eine Stelle im Array mit dem Wert 0 zeigt. Das Wort “a” (nicht im Bild) hat den Hash {1, 3, 4} und wäre gemäss Bloom-Filter enthalten. Es handelt sich um einen False-Positiv, denn wir haben das Wort nicht eingefügt.
Wie viele Hash-Funktionen verwendet werden müssen, kann berechnet werden. Dies hängt vor allem von der Grösse des Bit-Array und dieser wiederum von der Anzahl Elementen ab. Berechnet werden kann das relativ einfach. Die Wahrscheinlichkeit, dass ein Bit auf 1 gesetzt ist, ist \( \frac{1}{m} \) und folglich dass das Bit auf 0 bleibt ist dann \( (1 - \frac{1}{m}) \). Wenn mehrere Hash-Funktionen oder Elemente vorhanden sind, reduziert sich die Chance, dass das Bit auf 0 bleibt auf \( (1 - \frac{1}{m})^{kn} \). Die Wahrscheinlichkeit, dass alle Bit dann auf 1 stehen ist somit \( (1 - (1 - \frac{1}{m})^{kn})^k \), da k-Bits getestet werden müssen.
Die Verwendung eigener Hash-Funktionen ist gefährlich. Im obigen Beispiel geben die Hashfunktionen nur Werte von 0 bis 4 beziehungsweise 0 bis 5 zurück. Die Eigenschaft der Gleichverteilung ist somit verletzt. Das führt zu vielen False-Positiv-Ergebnissen sowie zu Platzverschwendung der anderen Speicherstellen, die 0 bleiben.